Appendix F

Octan Physics

 
[Fleegello originally wrote his critique of octan physics as section 2.3 of the Principia. It is listed separately here, as it frankly stands apart, and interferes with the general flow of that work. Most scholars agree that Fleegello did not introduce any novel physics in this section. Rather he took ideas already advanced by contemporary physicists, and adapted them to his own philosophical framework. Editorial comments are enclosed in brackets throughout the text, to distinguish them from primary content.]

The physical (pan)universe has been identified as the Physical Consistency Subfield (PCS) of the Consistency Ideo Field (CIF) – the complete set of abstract mathematical objects that both define physical (temporospatial) relationships and are compatible with consistency logic. The PCS may itself be naturally divided into multiple, logically self-contained physical universes, characterized by distinct physical laws and conditions. Our own universe would be one of these worlds.

Mathematical objects in the PCS may manifest (in part) as states of a physical system, or as operators representing observables or other entities that act on those states. If modern physics is a guide, they incorporate a broad class of multidimensional objects known as dimensors [including common scalars, vectors, more general tensors, and spinors]. Many useful dimensor operators (in particular, those representing observables) define linear relations between other dimensors.

In standard Shrodiik [quantum] theory [named in honor of the pre-Dracian physicist Shrodo], a physical state (of any sufficiently isolated system) is denoted by a ket symbol |ψ>, where ψ is an arbitrary label. This entity is supposed to encompass all physical aspects of a system. |ψ> was originally interpreted in terms of the positions and motions of material particles at a time t in a pre-existing three-dimensional (3D) space x [here bold type indicates a physical 3D vector]. Observables then include the positions, energies and momenta of these particles.

Contemporary Shrodiik physics has a most peculiar feature. For any physical state |ψ>, only the probabilities for measuring different values of a given observable can be computed. Even granted complete knowledge of a physical system at a particular moment, the future course as seen by any octan observer cannot in general be predicted with certainty. Detailed prescriptions for computing probabilities may be found in Shrodiik physics texts.

For any physical system, there is a range of possible states. Related to its probabilistic character, |ψ> can consist of a linear combination, or superposition, of these available states. The selection of a set of fundamental basis states is then arbitrary, to some extent; any given set of basis states can be mixed into new combinations, to form distinct sets.

In general, |ψ> can be viewed as a vector in an abstract space that spans all the possible states. If the components of a state vector are defined with respect to a specified set of basis vectors, then the state may be represented by a single-column dimensor array. Linear operators may in turn be represented by square dimensor arrays that transform any given state (by the rules of matrix multiplication) into another state.

Let  represent a (linear) operator corresponding to an observable A. Here the symbol "hat" explicitly denotes operator, versus numeric parameter, status. When  is applied to an arbitrary state vector, the result is typically a linear combination of other state vectors. Suppose, however, that  is applied to a state vector |ψ_a> characterized by a well-defined value a of A – i.e., a state in which a measurement of A will definitely yield the value a. Then  acts on |ψ_a> by extracting this value:

      Â|ψ_a> = a|ψ_a> .

This is what it means for  to represent an observable. Mathematically, |ψ_a> is an eigenstate of Â, with a well-defined value a of that observable.

From the perspective of a given observer, |ψ> evolves in a smooth manner until a measurement is made. Curiously, at this point |ψ> jumps discontinuously to an eigenstate corresponding to the measurement result. Performing a measurement (observation) abruptly reduces a system to an eigenstate of the observed quantity!

In bra-ket notation [physicists used this archaic script during Fleegello's era], the numeric overlap between two states |φ> and |ψ> is represented by <φ|ψ>, where the states are normalized such that <ψ|ψ>=1 for all |ψ>. The overlap value is a probability amplitude for starting with a system in state |ψ>, but observing it in state |φ>. The actual probability is the absolute square of this amplitude, or |<φ|ψ>|². For example, consider a one-particle system. If |x> is the state with the particle at 3D position x, then <x|ψ> is the wavefunction ψ(t,x) of Shrodiik mechanics, and |ψ(t,x)|² is the probability per 3D volume at time t for finding the particle at x. This is an absolute probability if ψ(t,x) is normalized such that the integral [a continuous sum over a volume of a function multiplied by an infinitesimal volume element] of |ψ|² over x is unity.

The expectation value of an observable A, defined as the average value A_avg over repeated measurements on identical states |ψ>, is given by

      A_avg = <ψ|Â|ψ> .

The observable A has a definite value a only if |ψ> is already an eigenstate |ψ_a> of Â.

In classical physics, material particles were treated as localized entities, distinct from waves (such as light) that propogate through underlying fields or media. Only waves could undergo self-interference, or diffract around obstacles. At the dawn of the Shrodiik revolution, ostensible particles were found to have wave properties, and nominal waves were found to sometimes act like classical particles. Observables that classically had a continuous range of values – e.g., the energy of an electron in an atom – might now be quantized, or restricted to discrete values.

Energy is one of the central observables in quantum physics. It is associated with the Hoobitean operator Ĥ [named for the classical physicist Hoobitu]. For material particles, Ĥ is often written as the sum of a kinetic energy term Ĥ_o plus a potential energy (interaction) term Ĥ_int. After wave-particle duality was discovered, the energy E of a (set of) particle(s) in an eigenstate of Ĥ became associated with a temporal frequency f, or angular frequency ω:

      E = ℎ f = ℎ ω / 2𝜋 = ℏ ω ,

where ℎ is the minuscule but nonzero Planko constant [named for the pioneering physicist Planko], and ℏ is the reduced Planko constant. Conversely, experiments showed that the energy in a traditional wave of frequency f was not continuously distributed over the wave, but carried by discrete quanta with individual energies given by the same equation. Ĥ embodies the way a state changes in time. When Ĥ acts on a state vector |ψ>, the result is the constant (iℏ) multiplied by the time rate of change of |ψ>, where i is the imaginary unit (square root of -1). It is remarkable how imaginary (or complex) quantities arise naturally in the equations of Shrodiik physics!

A 3D vector quantity closely related to energy is linear momentum, represented by the symbol p. Much as energy is associated with temporal frequency, momentum p_x along a spatial axis x is associated with a spatial frequency equivalent to an inverse wavelength λ_x or angular wavenumber k_x:

      p_x = ℎ / λ_x = ℏ k_x .

Shorter wavelength (and so either larger momentum, or a smaller value of ℎ) generally begets more particle-like behavior. When the operator p̂_x acts on a state vector |ψ>, the result is the constant (-iℏ) multiplied by the spatial rate of change of |ψ> along x.

For a single material particle, the relationship between time and energy is thus analogous to that between spatial position and linear momentum. For a multiparticle system, however, the situation is more nuanced. Whereas every particle may be assigned its own dynamical position and momentum operators, all particles traditionally share a common time. Time is then treated as a numeric system parameter, and not associated with a true operator.

Using calculus, it can be shown that the (unnormalized) time- and space-dependent wavefunction ψ(t,x) of a particle (or any quantum) with pure angular frequency ω and wavenumber k_x (energy E and momentum p_x) has the exponential, wave-like form

      ψ(t,x) = e^-iωt e^ik_xx = cos( k_xx-ωt ) + i sin( k_xx-ωt ) .

where e is the Eulero number of mathematics, and the "cos" and "sin" terms refer to standard trigonometric functions. More generally, for a 3D wavevector k (momentm p) and position x,

      ψ(t,x) = e^-iωt e^ik·x

where the scalar product  k·x is the scalar length of x multiplied by the projection of k onto x. Note that the relative probability at any moment for finding the particle at a given 3D position (equal to the absolute-square of the wavefunction) is the same for all x values.

With quantum physics, it is found that the order in which observables are measured may be significant. Consider then two observables A and B, represented by operators  and B̂. The observables/operators commute if the order of measurement is irrelevant, or equivalently if the order in which  and B̂ act on an arbitrary physical state is irrelevant – i.e., if ÂB̂ = B̂Â. They do not commute if ÂB̂ ≠ B̂Â. In this case the very act of measuring  or B̂ introduces uncertainty into the value of the other, complementary observable. A system cannot simultaneously be an eigenstate of two operators that do not commute – neither operator would alter such a state, so their order could not matter. It is then impossible to simultaneously measure the values of two non-commuting observables, since such a measurement must create an eigenstate of both.

In Shrodiik mechanics, the archetypal pair of observables with non-commuting operators are the position x and linear momentum p_x of a material particle along a given spatial direction. Classically, these quantities commute, and every particle simultaneously has well-defined position and linear momentum. Based on their operator interpretations, the quantum commutation relation between x̂ and p̂_x is

      x̂ p̂_x - p̂_x x̂ = iℏ .

Because the operators do not commute, an eigenstate of p̂_x must span a range of x values. As described earlier, an eigenstate of p̂_x is indeed totally unlocalized in space. Conversely, it can be shown that an eigenstate of x̂ must include all possible linear momenta p_x. More generally, if σ_x is the [standard deviation] uncertainty in x, and σ_px the uncertainty in p_x, it can be shown that

      σ_x σ_px ≥ ℏ/2 .

Consider then a system |ψ> = |x_o>, in which a particle initially has a definite position x_o. Suppose an observer measures first the position x of the particle, and then its momentum p_x. Because the system starts in a state of well-defined position, the particle will be found at x_o with 100% probability, and the wavefunction is unchanged. Because this wavefunction contains all possible momentum values, any value of momentum may be observed in the subsequent measurement, with equal probability. Now suppose the order of measurement is reversed – the observer measures momentum first, followed by position. The likelihood of initially observing any value of momentum p_x is the same as before. But the momentum measurement forces the particle into a state of well-defined momentum. The particle's position is thereby scrambled, and the observer may subsequently find the particle at any location!

Consider now a more general system in which one member of any pair of non-commuting observables is well defined. Mathematically, the system can be considered a superposition of pure eigenstates with different but well-defined values of the other non-commuting quantity. The existence of non-commuting observables is contrary to classical (pre-Shrodiik) physics. The natural law that describes physical evolution applies to superpositions of pure states, rather than to states in which all classical variables have precise values.

The state |ψ> of a physical system can in general be written as a coherent sum

      |ψ> = C₁|φ₁> + C₂|φ₂> + C₃|φ₃> + . . . = Σ_j C_j|φ_j>

over a complete set of orthonormal states |φ_j>, where the C_j are (complex) constants.

The |φ_j> are orthonormal if <φ_j|φ_k>=0 for all j≠k, and <φ_j|φ_j>=1 for all j.

The choice of the |φ_j> is arbitrary to some extent, but they must be eigenstates of a complete set of commuting observables that cover all physical aspects of the system.

The probability of starting with the system in state |ψ> but finding it in a state |φ_j> is then C_j^*C_j, where C_j^* is the complex conjugate of C_j. The expectation value of an observable A is

      A_avg = <ψ|Â|ψ> = Σ_jΣ_kC_j^*C_kA_jk   where A_jk = <φ_j|Â|φ_k> .

The off-diagonal terms j ≠ k in the sum represent nonclassical interference between the different states in the coherent superposition comprising |ψ>. These terms in general vanish only if the |φ_j> have well-defined values of A (i.e., are eigenstates of Â).

The physical interpretation of the state vector |ψ> has a long and tortuous history. Originally it was viewed merely as a device for computing the probability of observing a given outcome in an experiment. Reality was seen to reside in the observed positions and momenta of individual particles. The physical universe was assumed to evolve in a linear manner, with a single unfolding history, which was deterministic in only a limited, probabilistic sense. The act of observation was divorced from the natural evolution of a physical system, and treated as something special, even magical (the so-called measurement problem).

Yet consistency logic requires that the universe be totally deterministic. Recently, the contradictions inherent in the original interpretation of Shrodiik mechanics have led the Evette group to develop an alternative multi-world view, in which reality resides in |ψ> itself. Observers, measuring devices and related processes are now included as integral parts of |ψ>. The physical panuniversal |ψ> is viewed as a superposition of conventional quantum worlds, each represented by a restricted state vector, which have become decohered and mutually orthonormal [or minimally overlapping]. These worlds evolve [almost] independently of each other, and continually split [rarely merge] into new separate, decohered worlds through time. A given observer occupies one conventional world at a given instant. As this world subsequently splits, the observer likewise branches into multiple selves, each with a distinct future experience. An observer does not see physical evolution as completely deterministic simply because no individual mind encompasses all worlds of the unfolding panuniversal state.

[Unfortunately, only the barest references to the original Evette School survive in the historical record. The writings may have been systematically destroyed by conservative, fundamentalist religious sects that flourished at the time, and found the work heretical. These traditionalist factions believed the universe progressed in a linear fashion along a single preordained path, in accordance with a divine plan for the octan race. The random, branching character of the multi-world view demanded an even greater, and to many more threatening, decentering to the octan psyche than the recognition five octujopes earlier that Jopitar was not at the physical center of the universe, but was a nonsingular ball of ordinary matter orbiting a commonplace star adrift on a vast ocean of space and time.]

Let |ϕ₀> represent a conventional world in the Evette sense. Then the matrix elements A_0j between this world and any other coexisting conventional world |ϕ_j> must be [essentially] zero for all observables A, including noncommuting quantities. Such conventional worlds evolve independently, with no [minimal] mutual interference.

Suppose that |ϕ₀> incorporates a subsystem consisting of a simple superposition ( |B₁> + |B₂>) of orthonormal eigenstates of an observable B. Then

      |ϕ₀> = ( |B₁> + |B₂> ) |Ɛ>

where |Ɛ> represents the environment of the subsystem. The environment may interact with the subsystem, so as to become correlated with its eigenstates. This happens in particular when |Ɛ> includes an observer who measures the value of B. If B̂ commutes with the interaction Hoobitean Ĥ_int, the eigenstates of B̂ are not changed by the interaction, and

      |ϕ₀> ➜ |B₁> |Ɛ₁> + |B₂> |Ɛ₂> = |ϕ₁> + |ϕ₂>

where |Ɛ₁> and |Ɛ₂> are themselves eigenstates of observables that commute with Ĥ_int.

Consider now the matrix elements A₁₂ and A₂₁ with |ϕ₁> and |ϕ₂> for an arbitrary observable A. If  commutes with B̂, then A₁₂ = A₂₁ = 0, since the eigenstates of B̂ are orthonormal. If  does not commute with B̂, then it acts only on the B subsystem (if  were a product of operators that separately act on the subsystem and its environment, then A would not be a valid observable). In this case  does not affect |Ɛ>, and A₁₂=A₂₁=0 if |Ɛ₁> and |Ɛ₂> are orthonormal. The states |ϕ₁> and |ϕ₂> can thus be identified as two new conventional worlds, split off from the original |ϕ₀>, if only |Ɛ₁> and |Ɛ₂> are orthonormal.

[This line of reasoning, which did not originate with Fleegello, helped resolve a problem with the many-world interpretation, involving an apparent ambiguity in the identification of the individual worlds. Some researchers argued that the choice of states |B₁> and |B₂> in the given example was quite arbitrary. By choosing a rotated basis set, e.g.

      |b₁> = (|B₁> + |B₂>)/√2   and   |b₂> = (|B₁> − |B₂>)/√2 ,

the state |ϕ₀> appeared to split into a different set of conventional worlds. Eventually it was realized that the interaction between a system and its environment naturally selects a particular (compatible) basis set. If the operator B̂ does not commute with Ĥ_int, then |B₁>|E> does not evolve into |B₁>|E₁>, since |B₁> is itself transformed by the interaction.]

Conventional worlds can thus be distinguished by non-interfering "memories" of prior branchings. The storage sites of these data may include, but are by no means limited to, animal brains (and recently, scientific apparatus acting as extensions of those brains). The physical structure of a brain determines its interactions with the environment, and thus the types of conventional worlds (i.e., which observables are relevant and well-defined) generated by the observation process. If a brain is so constructed that only one value of a particular observable can communicate with (affect) other elements in a conscious field, then a state including a coherent superposition of different values of that observable at the same moment must correspond to distinct unified ideo fields, or selves, in separate (conventional) worlds. The information stored in a brain does not define the external reality of the associated world – a person may make faulty observations – but it may still be a point of reference by which that world is distinguished from others. Two distinct conventional worlds can even merge, if their distinguishing memories are lost or corrupted so as to become identical. Observers inhabiting the worlds would experience no sense of merger, as all valid memories of a former distinct past would be absent.

What determines useful observables, other than position? The mathematician Noethra has linked many such quantities to symmetries in the equations of motion that describe the temporal evolution of |ψ>. Noethra's first theorem states that for every continuous, differentiable coordinate transformation that does not alter these equations, there is a corresponding observable whose expectation value is conserved, or constant over time. For sufficiently isolated (closed) systems, the equations are in fact generally unaffected by several such transformations, including time displacement, spatial displacement, and spatial rotation. Each of these symmetries is associated with an observable and conserved quantity.

Why are the dynamical equations unaffected by the given transformations? Although physical conditions clearly vary at different locations in time-space, there is nothing else to distinguish points or directions. From an ideobasic perspective, physical law for a sufficiently closed system (which incorporates all relevant causal agents) should then depend only on extant physical conditions. Although distinct physical laws may apply in different physical universes, the same law and dependencies should apply at all times, positions and orientations within a given universe. This leads to the observed symmetries.

When the equations of motion are not affected by displacements in time (i.e., they remain the same over time), then what is commonly called energy is conserved. This is primarily what makes energy a useful observable. Note that only the laws of motion are unchanging; physical conditions and entire systems may change dramatically over time. When the equations of motion are not affected by displacements in spatial position (i.e., physical law is the same at different spatial points), then linear momentum is conserved, and is a useful observable. When the equations of motion are not affected by spatial rotations (orientation in space), then angular momentum is conserved, and useful. It can be shown more generally that the expectation value of any operator that both commutes with the Hoobitean operator Ĥ, and is not explicitly a function of time, is also a constant of motion. Every symmetry in Ĥ is thus associated with a conserved quantity, and a corresponding observable.

Classical observables may have nonclassical analogs that result from a reinterpretation (typically involving commutation relations) of associated operators. In particular, the commutation relations among the three orthogonal (mutually perpendicular) angular momentum operators imply the existence of a nonclassical type of angular momentum, known as spin. Elementary particles are found to inherently possess this type of angular momentum. Particle spin is naturally quantized to discrete values, characterized by a spin number s, which must be an integral multiple of 1/2. Overall spin angular momentum is ℏ√s(s+1), while the maximum possible component in any 3D direction is ℏs.

Spin angular momentum operators can be represented by irreducible (2s+1) x (2s +1) arrays. The spin aspect of a spin-s particle can then be represented by a (2s +1)-dimensional single-column dimensor known as a pointor, designated by Š. An overall single-particle state may in turn be represented by a pointor wavefunction Š(t,x) of time t and 3D position x.

Spinless (s=0) particles are represented by simple scalar (zero-rank dimensor) functions, with no inherent directionality. [No elementary spin-0 particles were known in Fleegello's era, although composite spin-0 particles (e.g., pions) were certainly recognized.] Spin-½ particles are represented by special two-dimensional pointors known as spinors. Spinors do not transform like geometric vectors under coordinate transformations. Spin-1 particles with mass are represented by three-dimensional pointors, which do transform like geometric vectors. [Because massless spin-1 particles (in particular photons) have no rest frame but are constrained to move at light speed, they must be represented by two-component pointors.] Particles with even larger spin values are represented by distinct pointor classes.

Yet particles do not normally exist in isolation. How then can the state of a multiparticle system be represented? Suppose first that the particles are distinguishable, and motions are much slower than light speed. Such systems have traditionally been represented by a direct product of the pointor functions for the individual particles, in which time t is a common system parameter, but the coordinates x_j of the various particles j are distinguished. For example, the state of a two-particle system might be represented by

      Š_a(t,x₁) Š_b(t,x₂) ,

where subscripts a and b label two different single-particle states.

Suppose now that two particles in a system are identical. The probability of finding either cannot be affected when their labels are exchanged – they would otherwise be distinguishable. Because the probability is equal to the absolute square of the wavefunction, and the associated exchange operator must (as an observable) be linear, the state can at most acquire a complex phase factor (absolute value one) under particle exchange. Since two successive exchanges must leave the state unchanged, the phase factor is limited to the values ±1. A state must then be either symmetric (unchanged) or antisymmetric (phase factor -1) under identical particle exchange.

The wavefunctions of identical bosons (particles with integral spin) are found to be symmetric, while those of identical fermions (particles with half-integral spin) are antisymmetric. The appropriate symmetry can be achieved if a system is represented by a sum over the direct pointor products, in which the functional dependencies of the particles are suitably interchanged. For example, the state of two identical fermions might be represented by

      Š_a(t,x₁) Š_b(t,x₂)-Š_a(t,x₂) Š_b(t,x₁) .

Symmetries in the equations of motion are not limited to continuous time-space transformations, but may also include discrete operations, such as time reversal and parity inversion (mirror reversal). [Fleegello stubbornly maintained that various discrete spacetime symmetries should generally hold, despite contrary evidence. For example, experiments seemed to demonstrate that parity is not conserved during certain types of radioactive decay. Parity is conserved if the equations of motion are unchanged when a system is replaced by its mirror image. Fleegello believed that physics could not be affected by such a simple transformation, and felt that crucial elements had been omitted from experimental analyses. Yet physicists soon realized that, since time and space are intimately linked, and antiparticles are equivalent to ordinary particles moving backward in time, the true symmetry involves the CPT transformation – a combination of particle-antiparticle charge exchange, parity inversion, and time reversal – and not any one of these operations in isolation.] Internal symmetries, that do not transform time-space points, can give rise to additional conserved quantities and observables (e.g., electric charge).

Indeed, the fundamental interactions between elementary particles are thought to derive from a variety of internal local gauge symmetries. For example, consider the electromagnetic interaction. Under a local phase transformation, the single-particle wavefunction ψ(t,x) is multiplied by a phase factor e^iλ(t,x), where λ(t,x) is an arbitrary function of time-space. The absolute square (probability density) of ψ is unchanged by this transformation. If local gauge symmetry holds, then the new wavefunction must also satisfy the standard equation of motion. The kinetic energy part of that equation generally contains terms involving both the time- and space-rate of change of ψ, so the phase factor in the transformed wavefunction generates new quantities. The equation is invariant under the transformation only if it also contains terms that transform so as to cancel the effect of the (t,x) dependence in λ, while maintaining the original form of the equation. These terms can be identified with the electromagnetic scalar and vector potentials.

The physicist Vigno has argued that symmetries do not merely restrict the laws of physics, but further define much of physical reality. While fundamental forces have been related to symmetries in the equations of motion, elementary particles have themselves been associated with (irreducible) mathematical representations of abstract symmetry groups. Every consistent object and process must coexist with every other consistent object and process somewhere within the PCS. This may involve a natural segregation into distinct, self-contained physical universes.

Coordinate systems do not exist a priori in nature. The choice of a coordinate framework to describe a physical system should thus be arbitrary, from a strictly mathematical viewpoint (although one frame may be more convenient than another for a given purpose). It should then be possible to describe the laws of physics in a coordinate-free manner, in which observables appear only as abstract quantities, with no explicit reference to coordinate components. Expressing physical laws in such a covariant manner simplifies identification of symmetries and conserved quantities.

If the PCS is to respect the inherent arbitrariness in the choice of coordinate system, then fundamental physical constants that appear in the laws of physics should also be the same for all observers within a given physical universe, independent of the choice of reference frame. This applies in particular to dimensionless constants (e.g., the fine structure constant of atomic physics), which carry no physical units, but can be expressed as the ratios or products of dimensional constants that do possess units. Changes in the values of dimensional constants are generally meaningful only with respect to changes in their dimensionless combinations. So long as the values of physical constants are individually changed in a way that maintains the values of all fundamental dimensionless constants, the physical world is unaffected. Dimensionless constants stand independent of any arbitrary choice of measurement units. Indeed, no variations over time or space have thus far been detected.

[Some quantities thought to be fundamental constants in Fleegello's era have since been found to be variable. These have been reinterpreted as functions of truly fundamental constants and local physical conditions.]

Dimensionless fundamental constants need only be the same at all points within a particular physical universe. The values in distinct, non-interacting universes may be different. If there is no fundamental reason a constant should have a particular value, then the PCS must encompass a host of universes covering the range of acceptable values. Yet these values should be countable (either discrete/quantized, or at least represented by rational numbers). All the worlds otherwise could not have meaningful existence within the PCS.

Even fundamental dimensional constants (whose numeric values depend on the choice of physical units) should be the same for all observers in a given universe, when measured with respect to reproducible units characteristic of fundamental physical processes. In particular, the speed of light in a vacuum, commonly denoted by the symbol c, appears to constitute a universal limit to the rate at which information can propagate through space. [Note that distinct limiting speeds for different types of information would lead to inconsistencies.]

As first proposed by the physicist Niestu in his theory of inertial invariance, the speed c has the same value for all observers, irrespective of their state of motion. This is contrary to classical expectations, whereby an observer moving toward (away from) a light source detects a higher (lower) relative light speed than an observer at rest with respect to the source. That c is finite may be expected from an ideobasic viewpoint. An infinite speed is a special, limiting case of a general value, and the PCS should opt for the least encumbered conception.

Niestu introduced a major paradigm shift in physics when he showed that a common value for c implies that time (space) intervals measured by one observer may be partially seen as space (time) intervals by an observer in a relative state of motion; time and space do not exist separately, but must be combined into a unified timespace [scientists of Fleegello's era apparently preferred this expression to today's more common term spacetime]. The effect is tiny at low velocities, but becomes significant as speeds approach c (so-called Niestiik speeds). The associated coordinate transformation between reference frames in a relative state of motion is distinct from that of classical physics. If the equations of motion are to remain invariant under a velocity transformation, then those equations must be modified as well. A remarkable consequence of inertial invariance is that any mass m is associated with an energy mc². For a free particle, the relationship between total energy E, momentum p, and rest mass m becomes

      E² = p²c² + m²c⁴ .

Niestu ultimately expanded his ideas into the theory of general invariance, which describes gravity in terms of distortions in the geometry of timespace.

[Fleegello overlooked a related serious inconsistency in his view of the CIF. The CIF must encompass all possible reference frames. If It experiences the same time as observers in those frames, as Fleegello envisioned, It must integrate the various time lines to maintain a single unified state of being. Yet if speed c is the same for all observers, events that are simultaneous in one frame may be nonsimultaneous in another. Events could then be seen by the CIF as both simultaneous and not simultaneous, a contradiction. This inconsistency is resolved only if the CIF transcends physical time, and experiences it the way corporeal creatures experience space – as block time. All events in the physical panuniverse then span a single, eternal moment in the mind of the CIF. Yet the CIF must still distinguish the time-like and space-like separations among physical events that define causal chains. Primacy resides in these causal chains, and not in the reference frames that observers use to describe them.]

While inertial invariance was readily incorporated into Shrodiik mechanics for single particles, problems arose for multi-particle systems. In particular, time and space coordinates were not treated coequally in the traditional equations of motion. Inertial invariance requires that time and position both be treated either as system parameters, or as formal operators. Currently the most widely adopted solution, based on the first approach, is to reformulate Shrodiik mechanics into a Niestiik quantum field theory (QFT), in which elementary particles of a given type are treated as quantum excitations of an underlying field. QFT covers both traditional particles with mass, like the electron, and zero-mass particles once considered pure waves, like the photon. Different particle types are represented by distinct fields, defined by a variety of attributes including rest mass, spin, and electric charge. For each field type, a position field operator and a conjugate momentum field operator, now functions of common timespace parameters (t,x), replace the single-particle 3D position and momentum operators x̂_j and p̂_j for the discrete particles j of Shrodiik mechanics. Because all fields share one time parameter, QFT (like Shrodiik mechanics) is a single-time theory (STT).

A simple field state in QFT is characterized by the number of (identical) quanta occupying each of a set of allowed levels. The number of quanta is just the number of "particles" of the given type. Field quanta contain no explicit particle labels; QFT respects the exchange symmetry of identical particles in a remarkably natural way. Indeed, in QFT it can be shown that fields with half-integral spin must be antisymmetric, and those with integral spin symmetric [dictated by the distinct Niestiik equations of motion for fermions versus bosons]. Many physicists prefer not to speak of particles at all in QFT, but only quanta. A general field state can be represented by a superposition of simple states. Unlike in Shrodiik mechanics, this is not limited to states with a fixed number of particles; interactions between fields result in the routine creation/destruction of quanta. The overall state of a system is represented by the direct product of its constituent fields, or more generally by a superposition of such products.

Shortly after QFT was introduced, the mathematician Draci proposed a multi-time theory (MTT) alternative, in which both the (observer-based) times and positions (t_j, x_j) of various particles j are now distinguished, and associated with coequal system operators (t̂_j, x̂_j). The earliest versions, identified here as MTTa, were simple extensions of Shrodiik STT. For a system of fixed N particles, and an observer in an inertial reference frame (t, x), the associated multi-time (MT) wavefunction has the form Ψ_mta(t₁, x₁; t₂, x₂; ...; t_N, x_N ). This reduces to the single-time (ST) wavefunction of Shrodiik mechanics if all the t_j are set to a common time t. Just as the ST wavefunction was defined over a constant-time surface, Ψ_mta is only defined over appropriate space-like hypersurfaces. As in Shrodiik STT, |Ψ_mta|² is a probability per unit 3N-dimensional (3ND) spatial volume. Normalization now requires that the integral of |Ψ_mta|² over all 3N spatial coordinates on a specified hypersurface equals unity.

A later version of MTT was a more radical departure from single-time theory, but more attuned to inertial invariance and the vagaries of measurement, and is adopted here. Every particle j in MTT has an innate proper time dimension, measured along the particle's world line. Different time lines are not inherently synchronized, but correlated only through interactions. To locate at time t_o the position x_j of particle j, an observer must interact with the particle at some particle proper time τ_j. Due to a synchronization ambiguity [Fleegello elucidates this point later], τ_j is not in general well defined for any given t_o and x_j. There must then be a probability distribution over a range of τ_j. Since there should be at least a probabilistic Niestiik-like transformation relating timespace coordinates (τ_j,0) in the particle rest frame to (t_j, x_j) in the observer frame, there is a corresponding distribution for t_j, centered on but not limited to t_o.

The wavefunction Ψ_mt must then separately incorporate the reference observer time t_o at which the (t_j, x_j) are measured, and feature a probability distribution over each t_j for any given (t_o, x_j). Inertial invariance requires an additional spatial coordinate x_o, paired with the temporal coordinate t_o. The functional dependence of the wavefunction is thus Ψ_mt(t_o, x_o; t₁, x₁; t₂, x₂; ...; t_N, x_N ). This function is a joint probability amplitude that, when the observer finds itself at time t_o, it somehow sees itself at x_o, and each particle j at t_j (corresponding to τ_j) and x_j. As in STT, Ψ_mt is defined over spacelike surfaces of constant t_o. But now Ψ_mt can be normalized in a Niestiik-invariant manner if only |Ψ_mt|² is a probability per invariant 4ND particle timespace (t_j,x_j) volume and 4D observer timespace (t_o,x_o) volume. The integral over all t_j, x_j, x_o, and an invariant range of t_o should then be unity. Because Ψ_mt is defined for single values of t_o, the integral over t_o makes physical sense only if there is a minimum proper time interval Δ, and the integral over t_o is confined to Δ at t_o.

Note that the new MT wavefunction Ψ_mt does not reduce to the ST wavefunction when all t_j are set to a common t_o. Times t_o and τ_j are not assumed to be well-correlated, though for non-Niestiik speeds it may be possible to set the average value of each t_j equal to t_o. Yet MTT does not posit that any material particle evolves along multiple time dimensions. Each particle j evolves along a single proper line τ_j. The corresponding t_j are observer-based, and measured with respect to a single observer time line. From the adopted MT perspective, a multiparticle system can be accurately described using one time coordinate only if t_o and the t_j are sufficiently correlated.

Unlike traditional Shrodiik physics, Ψ_mt incorporates an observer state, and so applies not only to external objects, but also to the observer itself. If the observer is a massive composite entity, x_omay be chosen to be the 3D position of the center of mass (COM) of its observing apparatus, within the observer’s frame of reference. It is natural for the observer to select an inertial observer frame centered on the average position of this COM. However, an inertial observer is free to select any frame moving at constant velocity relative to its COM rest frame. The overall wavefunction will then in general include not only a t_o-dependent energy term, but also an x_o-dependent self-momentum term. By summing over a range of states, it should be possible to localize x_o in Ψ_mt to values close to the COM.

It may seem exceptional that observer self-coordinates (t_o,x_o) refer to a composite macroscopic object, rather than a simple particle. Yet even the observed objects in Ψ_mt are not limited to elementary particles. Any object may be represented in Ψ_mt, so long as it can be treated like a single, unified entity within the given context and level of approximation.

Ψ_mt should evolve in a smooth manner, if all relevant processes are sufficiently modeled. This applies in particular to any measurement apparatus used by the observer. Most such devices are designed to select a single eigenstate of a specified observable, even if a system starts in a superposition of states. A measurement should then smoothly generate a superposition of decohered eigenstates, each with its own observer and measured value, as per Evette. However, measuring equipment is typically either not represented in Ψ_mt at all, or treated as a simple composite object characterized only by COM position plus a few other net quantities. Ψ_mt then cannot possibly capture the complex evolution of a system (including measuring apparatus) into a sum of decohered states, but must appear to collapse discontinuously during a measurement to an eigenstate of the measured quantity. Note that an observer’s experience is the same, however well measuring devices are portrayed.

From the perspective of particle j, the energy associated with particle j should be proportional to the time rate of change of Ψ_mt with respect to τ_j (with t_o and all other τ_k held constant). From the observer perspective, the energy of particle j is then proportional to the time rate of change of Ψ_mt with respect to t_j (with t_o and all other t_k constant). Because t_o derives from the observer’s own proper (rest-frame) time, then from the same perspective, the time rate of change of Ψ_mt with respect to t_o (with all t_j constant) should be proportional to the observer self-energy, and NOT the total energy of the system. The total system energy with respect to the observer is instead the sum of the individual particle energies, plus observer self-energy

If there are no particle interactions, Ψ_mt should separately satisfy the free-particle equations of motion for each particle j, as well as for the observer. If there are also no observer-particle interactions, then there is no way the observer can detect the particles, define observer-particle distances, or establish the relation between t_o and the t_j. Then Ψ_mt can only be a function of t_o and proper times τ_j. In this case, Ψ_mt can be constructed from products of independent, free energy eigenstates e^-iω_ot_o and e^-iω_jτ_j, where ω_o and ω_j are the angular frequencies associated with rest masses m_o and m_j of the observer and particle j, respectively.

If there are minimal observer-particle interactions but still no interparticle forces, Ψ_mt can be constructed from products of energy-momentum eigenstates e^{-iω_ot_o+ik_o·x_o} and e^{-iω_jt_j+ik_j·x_j}, where k_o and k_j are wavevectors corresponding to the (observer-based) momenta of the observer and particle j. Now ω_o and ω_j are frequencies associated with the overall energies of the observer and particle j. The observer has the same chance of seeing any t_j at a given t_o.

With interparticle forces, interaction terms must be introduced into the equations of motion, resulting in N+1 coupled equations of motion for an N-particle plus observer system. Draci has shown that, for any MTT, the respective interaction terms must satisfy a consistency condition, or the evolution of Ψ_mt along the various t_j is not well-defined.

Finding consistent MT equations with interactions is a challenge. Most notably, conventional interaction potentials always lead to inconsistency. Interactions must then be implemented by other means, in particular through the use of creation and destruction operators (defined to maintain appropriate symmetry under identical particle exchange), as in QFT. While the simplest forms of MTT are restricted to fixed N, use of these operators allows N to change.

It is often useful to adopt composite MT timespace coordinates to replace the (t_j,x_j). For an observer plus N=2 particles (j=1 or 2), define

      X = (a₁x₁ + a₂x₂)  and  r₁₂ = (x₂ - x₁) , where a₁ and a₂ are constants with (a₁+a₂)=1. Center-of-mass (COM) coordinates with a_j = m_j/(m₁ + m₂) are routinely used in non-Niestiik analyses of two-body systems. Analogous time coordinates may be defined, by

      T = a₁t₁ + a₂t₂  and  ρ₁₂ = (t₂ - t₁) .

At Niestiik speeds, center of momentum (also COM) coordinates are appropriate, with a_j = ω_j/(ω₁ + ω₂) for free particles. If the particles interact, individual energies E_j = ℏω_j ,are no longer constant, but a constant-velocity COM can still be defined.

The (t_o,x_o; t₁,x₁; t₂,x₂) are thus replaced by composite COM coordinates (t_o,x_o; T,X; ρ₁₂,r₁₂). Recall that (t_o,x_o) is already inherently composite, if the observer (including all measuring devices) is a macroscopic entity composed of myriad material particles. While this (t_o,x_o) could in principle be included in the definition of (T,X), and (t_o,x_o) replaced by coordinates with respect to a grand observer-plus-observed COM, such blurring of the observer with the observed is not generally useful in MTT.

The observer is nonetheless integrally connected to the observed two-particle system. Interactions between the observer and the particles define the COM motion of that system. If the particles are otherwise isolated, then ideally particle interactions determine the primary dependence of Ψ_mt on both ρ₁₂ and r₁₂, but interactions with the observer must inevitably have some residual effect.

The (T,X) and (ρ₁₂,r₁₂) each transform in the same way as any conventional (t,x). As long as (a₁ + a₂)=1, the rate of change of Ψ_mt with respect to T (with ρ₁₂ fixed) equals the sum of the rates of change of Ψ_mt with respect to t₁ and t₂ (with t₂ or t₁ fixed, respectively). The rate of change with respect to X (with r₁₂ fixed) is similarly the sum of the rates of change with respect to x₁ and x₂ (with x₂ or x₁ fixed, respectively). These results can be extended to N > 2 particles. Total particle energy E and momentum P, equal to the sums of the individual particle energies E_j and momenta p_j, are then proportional to the rates of change of Ψ_mt with respect to T and X, respectively. If every (x_j, p_j) and (t_j, E_j) form a pair of complementary, non-commuting operators, so do (X, P) and (T, E).

Energy / linear momentum eigenfunctions for two free particles can now be written

      Ψ_mt(free) ∼ e^{-iω_ot_o+ik_o·x_o} e^-iΩT+iK·X e^{-iω_ρρ₁₂+ik_r·r₁₂}

where (Ω,K)=(ω₁+ω₂, k₁+k₂) and (ω_ρ,k_r)=(a₁ω₂-a₂ω₁, a₁k₂-a₂k₁). Note that ω_ρ (and so all dependence on ρ₁₂) vanishes if a_j=ω_j (Niestiik COM)! The free eigenstate shows no preferred value of T, X, ρ₁₂ or r₁₂ at any t_o. More generally, interactions between the observer and the two-particle system determine the time correlation between t_o and T. Interactions between particles 1 and 2 determine not only the primary dependence of Ψ_mt on r₁₂, but also the correlation between t₁ and t₂, and so the dependence of Ψ_mt on ρ₁₂. For strong repulsive interactions, Ψ_mt should be significant only for large values of the Niestiik-invariant timespace separation S₁₂≡ √r₁₂² - c²ρ₁₂² . For strong attractive interactions, there should be solutions of Ψ_mt localized to small values of S₁₂. If t₁ and t₂ become tightly correlated, ρ₁₂ is confined to values near zero, and the particle-related time dependence of Ψ_mt is mainly through T.

Both QFT and standard MTT assume a pre-existing, observer-based, four-dimensional (4D) timespace framework (t, x). Even if this timespace is affected (warped) by matter and energy, it is not created by them. Yet what is the origin of timespace itself, and how are its coordinates meaningfully defined at all for a multiparticle system? Neither time nor space can be measured in absolute terms. Temporal and spatial intervals are gauged only with respect to physical processes and structures, which are traditionally interpreted in terms of elementary particles and their interactions. Stripped of these vestments, timespace loses all meaning. Physical objects and dimensions of relation are inextricably linked.

As mentioned earlier, every elementary particle with mass does have an innate proper time dimension. For every external observer time t_j in standard MTT, there is a corresponding internal proper time τ_j. Indeed, MTT can be formulated using the more fundamental τ_j. Yet because distinct proper time lines are not inherently synchronized, and correlated only by interactions, further temporospatial relationships can be defined only if particles interact.

Interactions corresponding to the fundamental forces are associated with gauge symmetries. In QFT, their description can be interpreted in terms of the exchange of phantom elementary gauge bosons by elementary fermions. The electromagnetic, weak, and strong interactions involve the exchange of phantom photons, W and Z bosons, and gluons, respectively (all spin-1). Phantom particles have all the attributes of their real counterparts, except mass; the usual relationship between energy, momentum and rest mass is not followed, making these particles ephemeral. Many physicists consider phantom particles not real in any sense, but merely a bookkeeping device. Elementary fermions include electrons, neutrinos, and quarks (all spin-1/2). [Fleegello's archaic list omits various forms of invisible matter, that interact with ordinary matter solely through the gravity.] Only the gravitational force, which is ostensibly associated with the exchange of phantom gravitons (spin-2, and normally massless), has eluded incorporation into the QFT framework.

While phantom particles were introduced in QFT, gauge symmetries in MTT should lead to expressions for interactions with an analogous interpretation. Because phantom bosons in either approach are superpositions spanning energies and momenta that do not respect standard mass relationships, their exchange should not be literally interpreted in terms of particle trajectories. Yet they do link interacting particles, and transfer information at light speed. Physical objects may also be linked and transfer information via real particles, though energy-momentum conservation in this case may require either composite particles or paired links. The exchange of either phantom or real particles can thus establish causal links (CLs) – phantom causal links (PCLs) or real causal links (RCLs), respectively.

Because individual particles can be identified in MTT, but not in QFT, fully exploiting CLs requires an MT approach. Consider then a CL of any type from particle j at proper time τ_j to particle k at τ_k. CLs are universal; all observers recognize the same connections, at the same proper times. CLs are directional; time (and information) flows forward or backward from one particle to another. This interparticle direction may be indicated by a binary parameter θ_jk=±1, where value +1 signifies forward flow from j to k, and -1 signifies reverse flow. Every [electromagnetic] CL can also be associated with a three-component (equivalent to a 3D) unit vector u_jk that defines a 3D spatial direction of flow at τ_k.

[While the parameter θ_jk is useful, it is not strictly necessary, as the information is already encoded in the temporal frequencies associated with the link. In quantum physics, a temporal phase factor e^-iωt indicates flow of positive energy along increasing time t when frequency ω>0. The factor e^{-iω_jk(τ_k-τ_j)} thus indicates flow of positive energy from j to k only when frequency ω_jk>0. If ω_jk<0, the factor can be rewritten as e^{-iω_kj(τ_j-τ_k)}, with frequency ω_kj=-ω_jk>0, indicating flow of positive energy from k to j. Thus only positive frequencies ω_jk and ω_kj are allowed for θ_jk=+1 and θ_jk=-1, respectively.]

Let an elementary event be any point on the world line of an elementary particle at which a CL is established with another particle. The physicists Machi and [later] Niestu have proposed that the network of CLs among particles does not merely occur within timespace, but even defines timespace. The number of spatial dimensions is just the number of components in u_jk. 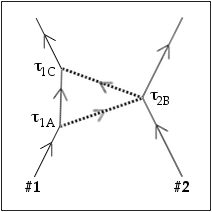For example, consider the pair of electromagnetic links between two charged particles #1 and #2 in the diagram at right. Suppose a CL (dotted line) connects #1 (solid line) at proper time τ_1A, defining event A, to #2 at τ_2B, marking event B; and a second CL connects #2 at τ_2B to #1 at τ_1C, or event C. Arrows point in the direction of time.

The location of particle 2 from the perspective of particle 1 (a non-inertial "observer" in this case) is

      r_12B = r_12B u_1AB

at time τ_1o = (τ_1A+τ_1C)/2, where u_1AB is a 3D unit vector pointing in the spatial direction of flow from A to B at τ_2B, and r_12B is the scalar interparticle distance

      r_12B = (τ_1C-τ_1A) c/2 .

From the same perspective, u_1BC = -u_1AB. Note that neither τ_2B nor the relative interparticle speed v appear in these equations. If τ₁ and τ₂ are not perfectly correlated (by the probability distributions for all possible interactions, which coincidentally define v), a range of τ_2B values could give the same result. τ_1B (which is not necessarily equal to τ_1o) should be related to τ_2B by at least a probabilistic, Niestiik-like (due to v-dependence) transformation. For non-Niestiik motion, one can set τ_1B~τ_2B based on the single interaction. However, τ_1B must equal τ_1o only if τ₁ and τ₂ are perfectly correlated. More generally, τ_1B has a range of possible values, corresponding to the range of τ_2B, but (with even minimal synchronization) centered on τ_1o.

From the perspective of #2, the situation is more nuanced. Timespace coordinates of event B are (τ_2B,0). It is not generally true that the two link paths are equal, or that u_2BC = -u_2AB. Interparticle distance r_21B at τ_2B now depends on v, with Niestiik corrections expected. While r_21B and v can be related to the times (τ_2A, τ_2B, τ_2C), deriving τ_2A from τ_1A, and τ_2C from τ_1C, depends on the correlation between τ₁ and τ₂. The interaction defines a definite correspondence τ_1o=τ_1B=τ_2B, with a common interparticle separation r_21B = r_12B, only if time is absolute (as in classical physics), and the time lines are synchronized.

Multiple serial links are required to correlate time lines and define interparticle distance over time. Yet the properties of successive links must be compatible, and accord with physical principles. In particular, adjacent CLs should reflect a consistent sense in the flow of time, or distance is ill-defined. Relative speeds must not exceed c. Changes in velocity (acceleration) should reflect the transfer of linear momentum by CLs.

Consider now the more general set of link pairs depicted at right, 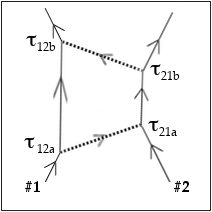again between particles 1 and 2. Introduce a new labeling scheme, whereby τ_jk is the proper time on the world line of particle j, for a link connecting j to k. Let ∩₁₂ represent the joint probability amplitude for the 1-2 link pairs, from the prespective of #1 (the first index), with functional dependence ∩₁₂ (τ_12a, τ_21a, θ_12a, u_12a; τ_12b, τ_21b, θ_12b, u_12b). Assume that ∩₁₂ is a complex quantity, and that the connection probability per τ_12a, τ_21a, τ_12b, τ_21b, solid angle in u_12a, and solid angle in u_12b is |∩₁₂|².

With respect to 1 at τ_1o, distance r₁₂ is defined by the special link pair AB and BC considered earlier, with τ_1A=τ_1o-r₁₂/c and τ_1C=τ_1o+r₁₂/c. These link pairs correspond to setting τ_12a=τ_1A, τ_21a=τ_21b=τ_2B, τ_12b=τ_1C, θ_12a=+1=-θ_12b, and u_12a=u_1AB=-u_12b in ∩₁₂. The joint ABC link-pair amplitude is then ∩₁₂ (τ_1A, τ_2B, +1, u_1AB; τ_1C, τ_2B, -1, -u_1AB). In terms of τ_1o and r₁₂, this is ∩₁₂ (τ_1o-r₁₂/c, τ_2B, +1, u_1AB; τ_1o+r₁₂/c, τ_2B, -1, -u_1AB).

The average of |∩₁₂|² over (r₁₂,u_1AB) for links ABC defines a probability distribution from the perspective of 1 at τ_1o that 2 is at time τ_2B, as well as the most probable value τ^p_2B, for any given τ_1o. The distribution width along τ_2B is a measure of the correlation between the time lines τ₁ and τ₂ at τ_1o, which is in general not one-to-one. Single-time theory then cannot most accurately describe the system.

Similarly, the average of |∩₁₂|² over (τ_2B,u_1AB) defines a probability distribution with respect to 1 that 2 is at distance r₁₂. As in standard Shrodiik physics, the width of this distribution may be nonzero even when τ₁ and τ₂ are well-correlated.

Remarkably, |∩₁₂|² for the link pair ABC has units equivalent [within a conversion factor c^-3] to a probability per 4D (τ_2B, r₁₂) timespace volume, just like the probability of an MT observer seeing particle 2 at τ_2B and r₁₂. Apart from an expected x₁ dependence, a CL-related partial wavefunction ɸ_mt can then be identified, with

      ɸ_mt(τ₁; τ₂, r₁₂) ~ ∩₁₂ (τ₁-r₁₂/c, τ₂, +1, r₁₂/r₁₂; τ₁+r₁₂/c, τ₂, -1, -r₁₂/r₁₂).

For any given τ₁, the quantity |ɸ_mt|² defines a joint probability distribution over (τ₂, r₁₂). Amplitudes should be normalized such that the integral of |ɸ_mt|² over all (τ₂, r₁₂) is unity.

In order to incorporate and interpret a variable x_o in the MT wavefunction ɸ_mt(t_o, x_o; ...), a student of Draci has proposed that a physical object may even have PCLs to itself. Consider the world line of particle 1, still from the perspective of 1. A self-link connecting τ_11a to τ_11b effectively extends out a distance r₁₁~(τ_11b-τ_11a)c/2 in direction u_1a1b=r₁₁/r₁₁ at τ_1o=(τ_11a+τ_11b)/2. The link-pair amplitude for a pair of self-links 1a-1b and 1c-1d may be written ∩₁₁ (τ_11a, τ_11b, +1, u_1a1b; τ_11c, τ_11d, +1, u_1c1d) defining a partial wavefunction

      ɸ_mt(τ₁, r₁₁) ~ ∩₁₁ (τ₁-r₁₁/c, τ₁+r₁₁/c, +1, r₁₁/r₁₁; τ₁-r₁₁/c, τ₁+r₁₁/c, +1, r₁₁/r₁₁).

Although particle 1 is not a classic observer, this ɸ_mt is defined from the perspective of 1, so (τ₁, r₁₁) is equivalent to (t_o, x_o) in ɸ_mt. The two links associated with ɸ_mt(τ₁, r₁₁) are indistinguishable, so r₁₁ is in effect defined by a single link rather than a pair of links. |ɸ_mt|² now has units equivalent to a probability per invariant 4D timespace (τ₁, r₁₁) volume, like any other link pair. The integral of |ɸ_mt|² over both r₁₁ and some invariant range of τ₁ should then equal unity for any τ₁. As discussed earlier for Ψ_mt, this makes physical sense only if there is a minimum proper time interval Δ, and the integral over τ₁ is confined to Δ at τ₁.

Self-links may occur along the world lines of classic observers, as well as ordinary particles. They thus offer a way to physically define observer self-distance x_o, just as link pairs define interparticle distances. Indeed, it may be that x_o is meaningfully defined only by self-links. Self-links may mark elementary particles as extended objects, and even embody classic force fields (e.g., the electric field of an isolated charged particle). As such, they would contribute to the rest-mass energies that dominate ɸ_mt in the low-interaction limit.

In a two-particle system, a self-link may become correlated with links between the particles, such that the corresponding joint link amplitude is not a product of two simple amplitudes. Let ∧_jk represent the full joint link amplitude, including all self-links, for CLs involving two particles j and k, where j and k are either 1 or 2 in the current example. Amplitude ∧_jk is functionally dependent on (τ_11a, τ_11b, θ_1a1b, u_1a1b), (τ_11c, τ_11d, θ_1c1d, u_1c1d), (τ_12a, τ_21a, θ_12a, u_12a), (τ_12b, τ_21b, θ_12b, u_12b), (τ_22a, τ_22b, θ_2a2b, u_2a2b), (τ_22c, and τ_22d, θ_2c2d, u_2c2d.

Based on its relationship with the standard wavefunction, it is convenient to now redefine ∩_jk as a truncated link-pair amplitude only including CLs with at least one end anchored to the world line of particle j (the first amplitude index). For example, ∩₁₂ includes link pairs 1-1 and 1-2, but not 2-2. While the full amplitude ∧_jk is a more complete representation of a system, ∩_jk can be derived from ∧_jk by appropriately averaging over extraneous link-pairs.

This scheme can be extended to systems with N>2 particles. Links between different particle pairs may become correlated, such that joint link amplitudes cannot be written as products of one- or two-particle amplitudes. The N=3 joint amplitude for particles 1, 2 and 3 may be written ∧₁₂₃, and includes links 1-1, 1-2, 1-3, 2-2, 2-3, and 3-3. The truncated amplitude ∩₁₂₃ includes links 1-1, 1-2, and 1-3.

Amplitudes ∩, ∧ and ɸ_mt should evolve in a smooth manner until a measurement is made. If they do not directly incorporate the measuring device, they must then discontinuously jump to eigenstates of the measured quantity. However, the role of observer is ambiguous here. Who performs a measurement – the reference particle, or a distinct external observer? The reference particle is not equipped to perform a classic measurement, and is a non-inertial platform. The ∩ and ∧ further utilize a mixed perspective, relying on proper times with respect to distinct particles. While proper times are independent of perspective, 3D directions and the values of quantities transferred by CLs are not. It is thus customary to express functional dependence in terms of quantities defined from a common perspective

In the traditional external-perspective MT (MTe) approach, a wavefunction is defined from the perspective of an inertial observer external to the system being examined. As described earlier, this observer is typically an organization of objects that establishes a common timespace framework, and provides a consistent perspective from which to survey a system. The observer should minimally perturb that system, except during a measurement. The position of a particle #1 is defined by CL pairs connecting the observer at t_o1 with the particle at t_1o, where t_1o is the most likely t_o (measured in the observer frame) corresponding to τ_1o. The full observer-based link-pair amplitude may be represented by Γ_o1 (including o-o, o-1, and 1-1 link pairs), and the truncated amplitude by γ_o1 (with only o-o and o-1 pairs).

Truncated MTe amplitudes generally embody all information directly accessible to an external observer by measurement. The γ_o1 defines a partial wavefunction

      ɸ_o1(t_o, x_o; t₁, x₁) ~ γ_o1 (t_o-x_o/c, t_o+x_o/c, +1, +x_o/x_o; t_o-x_o/c, t_o+x_o/c, +1, +x_o/x_o;
                                                                 t_o-x₁/c, t₁, +1, +x₁/x₁; t_o+x₁/c, t₁, -1, -x₁/x₁) .

The MTe formalism is readily extended to N>1 particles. For a pair of particles 1 and 2, link-pair amplitudes are Γ_o12 and γ_o12, defining ɸ_o12(t_o, x_o; t₁, x₁; t₂, x₂). Links involving only 1 and 2 are defined in Γ_o12, but not γ_o12. Now ɸ_o12 defines a joint probability that the observer at t_o sees itself at x_o, particle 1 at (t₁, x₁), and particle 2 at (t₂, x₂). Units of |ɸ_mt|² are probability per 4D (t_o, x_o) spatial volume for the observer (defined over interval Δ at t_o), and per 4D (t_j, x_j) timespace volume for every other j (defined over all t_j).

When averaging over link pairs to derive γ from Γ, information is lost. Truncated link-pair amplitudes are nonetheless indirectly affected by processes explicitly represented only in the full link-pair amplitude. For example, even though the truncated amplitude γ_o12 does not directly include any 1-2 links, the o-1 and o-2 link pairs defining the joint probability amplitude for observer-particle vectors x₁ and x₂ effectively defines the amplitude for the interparticle vector (x₂-x₁).

When deriving γ from Γ, it may sometimes be useful to either retain or discard extra information. An alternate truncated link amplitude γ^~may then be defined, that contains more or less information than the standard amplitude γ, and is associated with an alternate partial wavefunction ɸ^~. For example, suppose a wavefunction for particles 1 and 2 is desired that retains direct information concerning all self-links. Then an amplitude γ_o12^~ excluding only 1-2 link pairs can be derived from Γ_o12, defining the alternate partial wavefunction ɸ_o12^~(t_o, x_o; t₁, x₁, x₁₁; t₂, x₂, x₂₂). Here ɸ_o12^~is a joint probability amplitude that the observer at t_o sees itself at x_o, particle 1 at (t₁, x₁) with a self-displacement x₁₁ (at t₁₁=t₁ in Γ_o12), and particle 2 at (t₂, x₂) with a self-displacement x₂₂ (at t₂₂=t₂ in Γ_o12). Units of |ɸ_o12^~|² are probability per 4D (t_o, x_o) observer timespace volume (defined over interval Δ at t_o), per 4D (t_j, x_j) timespace volume for j=1 and 2 (defined over all t_j and x_j), and per 4D (t_jj, x_jj) timespace volume for j=1 and 2 (defined over Δ at t_jj=t_j).

The probability configuration of a multiparticle system evolves in time, whether or not it is watched by an external observer. Ideally, the configuration in MTe evolves independently of the observer, except when a measurement is made. As discussed previously, even then it is unnatural that the wavefunction collapses non-deterministically. To avoid wavefunction collapse, and pursue a more complete, self-contained theory in which CLs independently generate timespace, an alternate internal-perspective MT (MTi) approach may be adopted. Such an approach neither presumes a classic external observer, nor relies on a pre-existing 4D timspace, but assumes only that every particle has an innate proper time, and that CL (gauge) bosons are associated with mathematical objects that define common multi-D properties.

One version of MTi is an extension of MTe, in which the measuring device is explicitly included and modeled in Γ, such that the associated wavefunction does not appear to collapse when a measurement is performed, but instead separates into a sum of decohered states. The external inertial observer thus becomes an internal inertial observer. It is not necessary to model the measuring device in detail, but only to the extent that the wavefunction properly evolves into a sum of decohered eigenstates of the measured quantity during a measurement.

A second version of MTi is an extension of the original ∩ scheme. Because ∩ relies on proper times with respect to distinct particles, it is inherently covariant in time, but utilizes a mixed perspective. Other quantities must still be defined with respect to some reference frame. In the new MTi approach, times and other quantities are now all defined from the consistent but non-inertial perspective of a given particle, indicated by the first index in the link-pair amplitudes. For two particles 1 and 2, the full MTi link-pair amplitude Γ₁₂ with respect to particle 1 covers links 1-1, 1-2 and 2-2, while the truncated γ₁₂ covers only links 1-1 and 1-2. All times are measured with respect to the proper time of particle 1, so t_1j=τ_1j, andt_2j is the most probable time along the world line of particle 1 corresponding to τ_2j, for j=1 or 2. Note that for any (τ₁₂,τ₂₁) there is a probability distribution over t₂₁ , and for any (τ₁₂,t₂₁) a distribution over τ₂₁, defined by Γ₁₂. Amplitude γ₁₂ defines a partial wavefunction ɸ₁₂(t₁, r₁; t₂, r₂) in the usual way, except that now particle 1 replaces an external observer. ɸ₁₂ is a joint amplitude, from the perspective of particle 1 at t₁, that 1 is at r₁ and 2 is at (t₂, r₂). The system may equally be represented by ɸ₂₁(t₂, r₂; t₁, r₁) from the vantage of particle 2, with amplitudes Γ₂₁ and γ₂₁. While the perspective in this approach is inherently non-inertial, an inertial perspective may be achieved by transforming quantities to a COM reference frame. Classic measurements remain problematic in this MTi version, as there is no capable observer.

For systems with N>2 particles, link pairs may be correlated, such that CL amplitudes cannot be encoded using two-particle Γ_ojk and γ_ojk, or Γ_jk and γ_jk. For N=3 particles 1, 2 and 3, it is necessary to introduce correlated link-pair amplitudes Γ_o123 and γ_o123, or Γ₁₂₃ and γ₁₂₃. Information regarding links not involving the observer is found in Γ_o123, but not γ_o123. Similarly, information regarding links not involving particle 1 is in Γ₁₂₃ but not γ₁₂₃. The corresponding partial MTi wavefunction is represented by ɸ₁₂₃(t₁, r₁; t₂, r₂; t₃, r₃). The system may equivalently be represented by ɸ₂₁₃ or ɸ₃₁₂, from the perspectives of 2 or 3.

What are the functional forms of the link-pair amplitudes and wavefunctions in MTT? The explicit functional dependence ultimately derives from the MT equations of motion, which have not yet been identified. However, it is still possible to explore features expected of actual solutions, and to tentatively consider quasiphysical functions which embody these features. Consider then an MTe system consisting of an observer plus a single particle #1. Let γ_o1 (t_ooa, t_oob, θ_oaob, u_oaob; t_ooh, t_ood, θ_ocod, u_ocod; t_o1a, t_1oa, θ_o1a, u_o1a; t_o1b, t_1ob, θ_o1b, u_o1b) be the truncated link-pair amplitude covering both o-o and o-1 links, and ɸ_o1(t_o, r_o; t₁, r₁) the associated partial wavefunction. All quantities are defined from the observer perspective.

It is useful to express both γ_o1 and ɸ_o1 as products γ_o1 = γ_free γ_int and ɸ_o1 = ɸ_free ɸ_int of free-particle and interaction terms. In the weak (free-particle) interaction limit, we expect

      ɸ_free ∼ Ψ_free ∼ e^{-iω_ot_o+ik_o·x_o} e^{-iω₁t₁+ik₁·x₁}

where (ω_o,k_o) and (ω₁,k₁) correspond to (energy, momentum) of the observer and particle, respectively. Here ℏ²ω² = ℏ²k²c² + m²c⁴ separately for the observer and particle, if m is invariant rest mass.

This free-particle behavior in ɸ_free can be reproduced by setting γ_free to a product of factors, one for each link (four total), where each factor is in turn the product of an exponential temporal and an exponential spatial frequency term. For observer self-links oa-ob and oc-od, the temporal terms have a common frequency ω_o/2 and time variables (t_ooa+t_oob)/2 or (t_ooc+t_ood)/2, while the spatial terms have a common wavevector k_o/2 and space variables x_oaob=c (t_oob-t_ooa) u_oaob/2 or x_ocod=c (t_ood-t_ooc) u_ocod/2, respectively. For observer-particle links o1a and o1b, the temporal terms have a common frequency ω₁/2 and time variables t_1oa or t_1ob, while the spatial terms have a common wavevector k₁/2 and space variables x_o1a=c (t_1oa-t_o1a) u_o1a or x_o1b=c (t_1ob-t_o1b) u_o1b, respectively. Here x_o1 is a 3D distance vector from the observer to particle 1, defined separately for each link at t_1o.

The link frequencies corresponding to (ω_o,k_o) and (ω₁,k₁) can be interpreted as properties of the observer and particle 1, respectively, and not quantities transferred by CLs. This is consistent with minimal interactions. Yet interactions between the observer and itself, or the observer and particle 1, may cause information transfer along links, and determine γ_int.

Consider such a link pair between the observer and particle 1. Define δ_o1 ≡ θ_o1 (t_1o-t_o1), the forward time displacement between the observer and particle 1 along link o1a or o1b. Let ω_o1>0 be the temporal frequency associated with energy transfered along δ_o1, and k_o1 the wavevector associated with linear momentum transfered in the same direction. Mathematically, a summation ∑_ωe^-iωt over a range of ω peaks at t∼0. If interactions correlate t_o and t₁, then |γ_int| should peak at some δ_o1 ∼ d₁/c, where d₁ is a 3D distance vector that is in general a function of t₁. If x_o1 is bounded, |γ_int| should also peak at x_o1∼d₁. The functional dependence of γ_int can then be approximated by a product of two 4D sums

      γ_int ∼ ∑_ωo1ae^{-iω_o1a(δ_o1a-d₁/c)} ∑_ko1ae^{+ik_o1a·(x_o1a-d₁)} ∑_ωo1be^{-iω_o1b(δ_o1b-d₁/c)} ∑_ko1be^{+ik_o1b·(x_o1b-d₁)}

over a range of (ω_o1a,k_o1a) and (ω_o1b,k_o1b) for links o1a and o1b, respectively.

What is the functional behavior of the corresponding ɸ_int(t_o, x_o; t₁, x₁)? Define a time correlation parameter ε_o1=(t₁-t_o) and an associated vector ε_o1=ε_o1(x₁/x₁), where x_o1=x₁+θ_o1cε_o1 when t_o1a=t_o-x₁/c, t_o1b=t_o+x₁/c, and t_1oa=t_1ob=t₁. Then

      ɸ_int ∼ ∑_ωo1ae^{-iω_o1a(cε_o1+x₁-d₁)/c)} ∑_ko1ae^{+ik_o1a·(cε_o1a+x₁-d₁)} ∑_ωo1be^{-iω_o1b(-cε_o1+x₁-d₁)/c)} ∑_ko1be^{+ik_o1b·(-cε_o1a+x₁-d₁)} .

This function peaks at ε_o1∼(d₁-x₁)/c and ε_o1∼(d₁-x₁)/c for link o1a, but ε_o1∼(x₁-d₁)/c and ε_o1∼(x₁-d₁)/c for link o1b, or overall at t₁∼t_o and x₁∼d₁, as expected with interactions.

Consider now an observer interactive self-link pair. Define δ_oaob=θ_oaob(t_oob-t_ooa) and δ_ocod=θ_ocod(t_ood-t_ooh), the forward time displacement along observer self-links oa-ob and oc-od, respectively. Let ω_oo be the temporal frequency associated with energy transferred along δ_oo, and k_oo the wavevector associated with linear momentum transfered in the same direction, for each link. Suppose that the functional dependence of γ_int with respect to observer self-links can be approximated by a product of two 4D sums

      γ_int ∼ ∑_ωoaobe^{-iω_oaobδ_oaob} ∑_koaobe^{+ik_oaob·x_oaob} ∑_ωocode^{-iω_ocodδ_ocod} ∑_kocode^{+ik_ocod·x_ocod}

over a range of (ω_oaob,k_oaob) and (ω_ocod,k_ocod) defined separately for each self-link oa-ob and oc-od. The corresponding ɸ_int peaks at x_o~0, corresponding to the observer seeing itself localized at the origin of the observer coordinate system.

By using generalized link amplitudes that include both free-particle and interaction terms, partial wavefunctions ɸ_mt can be made equivalent to the complete wavefunction Ψ_mt. To the extent they define this wavefunction, links essentially define timespace itself. When interactions are considered, γ_o1 includes dependence on (ω_oaob,k_oaob), (ω_ocod,k_ocod), (ω_o1a,k_o1a), and (ω_o1b,k_o1b), in addition to (ω_o,k_o; ω₁,k₁). The link-pair probability per dependent quantity is again |γ_o1|².

[Fleegello unnecessarily restricted each CL to the transfer of a single quantum of information. A link may actually transfer any number of information packets, each a superposition of frequency (or other) states. A link amplitude must specify the number of packets, as well the link type (PCL or RCL) and the state superposition distribution associated with each. Amplitudes may alternatively be reformulated in a way resembling QFT, to specify the number of quanta occupying each of a set of link states.]

Return to link pairs o1a and o1b between the observer and particle 1. What are the restrictions on transferred quantities? Energy and momentum should be conserved at every link vertex. In the case of RCLs (e.g., an observer may scatter a real photon from particle 1 to see where and when it is), then only t_o1a=t_01b (link pairs defining the wavefunction ɸ_int) is allowed if particle 1 is elementary. Quantities ω_o1 and k_o1 must further satisfy the standard relation between temporal frequency, wavenumber, and rest mass of the link particle along each link.

For PCLs, energy-momentum conservation requires that the effective link mass for a solitary link be imaginary, if particle 1 is elementary. This is allowed, as PCLs are transient, and represent only the effect of a force field, not actual particles. Although information moves at light speed, the relation between ω_o1 and k_o1 is not constrained. Because a negative frequency ω_o1 moving in the positive time direction is equivalent to a positive frequency moving in the opposite θ_o1 direction, physically meaningful ω_o1 can be restricted to positive values.

Momentum wavevectors k_o1 may in general contribute to ɸ_int even when they point in directions other than u_o1=θ_o1x₁/x₁. Whereas the average value of k_o1 should be collinear with u_o1 for RCLs, this restriction does not apply to PCLs. The quantity k_o1 presumably contributes to changes in the velocity of particle 1 seen by the observer. Define k⁺_o1 to be the component of k_o1 along u_o1, with k⁺_o1=k⁺_o1u_o1. The philosopher Puuliin has suggested that forward wavenumbers k⁺_o1u_o1 must be positive if an interaction is repulsive, and negative if it is attractive. k⁺_o1u_o1 respectively points in the same direction as u_o1, or in the opposite direction.

How closely can the proposed product of two 4D sums of frequency eigenfunctions in γ_int correlate t_o with t₁, and x₁ with d₁? In addition to the time correlation parameter ε_o1, define a 3D distance correlation vector η_o1=x₁-d₁ at (t_o,t₁). In the classical limit, t_o and t₁ can be perfectly synchronized, and a unique 3D distance d₁(t₁) exists at t₁ . The quantities ε_o1 and η_o1 are then both zero with 100% probability. The corresponding γ_int can be approximated by a maximal summation over (ω_o1a,k_o1a) and (ω_o1b,k_o1b) eigenfunctions. In the classical extreme, the sum is over discrete values of ω_o1 from 0 to +∞, and each component of k_o1 from -∞ to +∞ (including zero), at increments Δω_o1 and Δk_o1, in the limit Δω_o1→0 and Δk_o1→0. Each phase factor in the sum is multiplied by the four-dimensional product of the increments.

[This sum is comparable to the product δ(ε)  δ³(η) of four Draci delta functions, where δ(x) is defined by δ(x) = 0 for x≠0, and δ(0)=∞ such that the area under δ(x) is unity. δ³ is the product of three ordinary delta functions, one for each spatial component of η.]

Can such a link amplitude be realized in our physical world? RCLs and PCLs actually have distinct minimum and maximum allowed absolute values (ω_min, ω_max) of angular frequency and (k_min, k_max) of wavenumber in any superposition of simple states.

For real massless bosons, an RCL travel distance d₁ defines a limiting maximum wavelength λ_max=2d₁, entailing a minimum frequency ω_min=𝜋c/d₁ and wavenumber k_min=𝜋/d₁. Limiting maximum values of frequency and wavenumber are defined only by the (inverse) smallest meaningful size of a timespace interval, and so are presumably huge but finite.

The situation is reversed for PCLs. Because a PCL represents collective phantom processes and does not comprise an independent time line, phase cannot gradually change along its length; only the net shift is meaningful. This shift must then be limited to the range -𝜋 to +𝜋. Any outside value would be indistinguishable from a number inside the range. A PCL travel distance d₁ thus defines a limiting maximum absolute frequency ω_max=𝜋c/d₁ and wavenumber k_max=𝜋/d₁.. The minimum frequency and wavenumber are both zero.

For RCLs, the ω_o1 and k_o1 must further satisfy the standard Niestiik energy–momentum relationship with rest mass (zero for a massless boson link), and both ω_o1 and k⁺_o1 are restricted to positive values. For PCLs, ω_o1 must also be positive, and k⁺_o1 may be restricted to positive (negative) values if an interaction is repulsive (attractive).

A PCL sum may not favor all frequencies and momenta equally within the allowed ranges. Analogous sums in QFT electromagnetic calculations include factors like 1/(ω²-c²k²), favoring photon-like states with effective mass near zero. Applying appropriate limits, but neglecting any weighting factors, a sum can be converted to an integral, and evaluated using calculus. Probability distributions may be derived from the absolute squares of the results.

Absolute squares of the sums over ω_o1a, k_o1a, ω_o1b and k_o1b for links o1a and o1b yield partial distributions P_o1aω(ε_o1+x₁-d₁), P_o1ak(ε_o1+η_o1), P_o1bω(ε_o1-x₁+d₁), and P_o1bk(ε_o1-η_o1) respectively. The overall joint probability distribution P(t_o,t₁,x₁,d₁) is the product of these partial distributions. For simplicity, write ε≡ε_o1 and η≡η_o1, and evaluate the restricted probability distribution P(ε) at η=0, the peak of P(η). Note that all four sums over both temporal and spatial frequencies contribute to the distribution, and that |ε_o1|=|ε_o1| exactly. The distribution P(η) may similarly be evaluated at ε=0, the peak of P(ε). Although in general |x₁-d₁|≠|x₁-d₁|, we can approximate |x₁-d₁|=η~|x₁-d₁| when evaluating P(η), underestimating the width of the distribution somewhat.

For PCLs, if wavevectors are not limited to k⁺_o1≥ 0 or k⁺_o1≤ 0, the distribution P_PCL(ε) is

                      sin⁴(ω_maxε/2)    [k_maxcε cos(k_maxcε) - sin(k_maxcε)]⁴
      P_PCL(ε) ∼  ^{____________    _______________________________}  ω_max N_ε
                          (ω_maxε)⁴                       (k_maxcε)¹²

where N_ε is a dimensionless normalization constant, and both ω_min and k_min are set to zero. If ω_max=k_maxc, then N_ε≅560. This distribution is symmetric in ±ε, and peaks at ε=0 with a value 0.4ω_max. The uncertainty in ε (∼0.5 the distribution full width at half maximum) is σ_ε∼1.1/ω_max. For PCL limiting frequencies, the peak value is 1.3c/d₁ and σ_ε∼0.35d₁/c.

If the k⁺_o1are restricted (as per Puuliin) to either positive or negative values, the integrals over k_o1a and k_o1b become more complicated. The distribution is still symmetric in ±ε, but with a broader width, and an uncertainty σ_ε∼1.5/ω_max. For PCL limiting values, σ_ε∼0.5d₁/c.

The distribution P_PCL(η) has the same form as P_PCL(ε) to the extent that |x₁-d₁|∼|x₁-d₁|, except now η≥0 and so N_η≅2N_ε. The uncertainty in η is σ_η≥cσ_ε.

For RCLs, there is no explicit integration over ω_o1, as it is folded into the integration over k_o1. For massless boson links, ω_o1=c k_o1. The distribution P_RCL(η) is comparatively complicated, but again peaks at ε=0, with an uncertainty σ_ε∼2.4/ω_max. However, the ω_max=c k_max limit is much larger than for PCLs. The distribution P_RCL(η) is related to P_RCL(ε) as with PCLs.

!!!!!

The correlation between t_o and t₁ is thus in general not one-to-one, especially for PCLs. As long as elementary physical objects have separate world lines (this conclusion then applies to MTT, but not QFT), STT is an approximation; a multi-time scheme must be more accurate. The classical limit is approached only through a sum of lower-energy PCLs and higher-energy real boson links. The minimum uncertainty in the correlation between t_o and t₁ from phantom processes alone is ~d₁/c (the time light travels d₁). An uncertainty ~d₁ is likewise inherent in any PCL specification of interparticle distance. Values for a macroscopic observer viewing a single fermion could be much smaller, if real particles are used as probes.

The precise form and time evolution of MT causal link amplitudes and wavefunctions are ultimately defined by dynamic equations of motion. What are these equations, and . . .
.
 
.
 
.
 
.
 

[At this point there is a gap in the historic record, in which Fleegello purportedly tried to formulate a regorous mathematical framework for MTT, and demonstrate that CLs provide a complete, novel MT framework for representing multi-particle systems. His failure to complete this project apparently led Fleegello to doubt his own competence and worth as a natural philosopher / physicist, and to destroy all related material in a fit of despair shortly before his death.

Physicists eventually did develop a complete MTT that supplanted standard single-time QFT. Here the connections among elementary non-gauge particles (mainly fermions, plus non-gauge bosons unknown to Fleegello) inherently define spacetime, and PCLs are dictated by MT gauge symmetries. For every non-gauge particle type, there is a pair of operators that create or destroy, respectively, one such particle, including its own proper time line (typically beginning and ending on the world line of another non-gauge particle, e.g. during a collision). For every gauge boson, there is a pair of operators that create or destroy, respectively, a CL between two specified points on particle world lines. Operator commutation relations ensure the appropriate symmetries of quantum states.]

Insofar as CLs specify 3D direction vectors, they also define (probability amplitudes for) the relative 3D positions of all causally connected particles in a system, regardless of their number. Yet CLs should be capable of establishing a 3D spatial framework even without these inherent 3D direction vectors.

Consider in this regard an isolated system of N distinguishable particles. If relative speeds are non-Niestiik, then interparticle distances d_jk ≅ d_kj, and CLs define amplitudes for N(N-1)/2 such distances. These are sufficient to construct amplitudes for the (3N-6) coordinates of 3D interparticle relative position vectors (up to a rigid rotation and displacement of the entire system), as long as N>3. Indeed, they should be sufficient to determine all relative coordinates for up to (N-1) dimensions. Relative speeds and accelerations are implicit in changes in the d_jk along world lines. Comparable conclusions apply even to quantum systems of identical particles, and for Niestiik speeds.

The web of CLs and associated proper times among the world lines of elementary particles could thus determine the geometry of timespace, in particular the large-scale geometry, whether or not CLs specify spatial direction. In either case, space can unfold from the relationships among myriad connected events. To the extent this occurs, space does not have independent existence, but is defined by the connections between the mathematical objects we perceive as particles. A world without causal links would be a world without space; any particles would be independent of each other, with no meaningful positional relationships.

Yet why do inter-particle connections defined by interactions specifically generate an overall three-dimensional, nearly flat (under normal conditions) space? Classically, even without inherent 3D directions, the N(N-1)/2 interparticle distances in an N-particle system are sufficient to determine all relative coordinates for up to (N-1) dimensions!

The mathematical physicist Wittuu has proposed a mechanism that both restricts and defines the number of spatial dimensions. Large-scale timespace is defined mainly by the electromagnetic interaction, since it is associated with the exchange of phantom photons of unlimited range. While real photons are massless, and so restricted to two spin states, phantom photons have three spin states, like any spin-1 particle with mass. These correspond to three inherent, independent "directions." Because all photons are identical, exchanging their identities cannot alter a physical system, so they must share the same three directions. Every interparticle distance defined by photonic CLs is thus limited to vectors in a common 3D space.

The strong and weak interactions should establish additional spatial dimensions. Although there are eight gluon types, these are not truly independent, and together generate only three new dimensions. The three bosons of the weak force generate the same, making a total of nine spatial, or ten timespace dimensions. Yet the ranges of the strong and weak interactions are so tiny (~10^-13 and 10^-16 centurets, respectively), they mainly affect the small-scale geometry of timespace. Wittuu suggests that the associated dimensions are "curled up" or "attenuated," and only obvious at very small scales or high energies.

[While Wittuu's argument was sketchy, later generations of physicists demonstrated that his intuition was sound (although he missed a few small-scale dimensions). A rigorous explanation of the origin of macroscopic spatial dimensions was eventually developed. Spacetime essentially arises as an emergent property from the interconnections among primitive, abstract, timeless mathematical forms.]

What about gravity? The carrier of this interaction is ostensibly the massless graviton. Because the graviton is a spin-2 particle with unlimited range, gravity might be expected to generate its own large-scale 5-dimensional space. Yet gravity has an unusual character, related to its incompatibility with standard QFT. All other fundamental forces are carried by spin-1 bosons, and associated with unique and conserved "charges" (e.g., electric charge). But gravity couples to a system's stress-energy tensor, to which every interaction contributes. Gravity reduces all "bare" mass energies, and even couples to itself, leading to nonlinearities in the gravitational field equations. PCLs established by gravity are thus dependent on and flow from the other interactions, so that gravity does not add any new dimensions. It may nonetheless distort the large-scale structure of timespace, as in Niestu's theory of general invariance.

It is clear that neither standard graviton exchange nor general invariance represents the complete fundamental description of gravity, even if both are good approximations in the low-energy limit. A missing element in these theories may involve the small-scale structure of time. Physicists have traditionally considered time to be continuous. In an attempt to avoid divergent (infinite) quantities in QFT calculations [which had previously been removed for forces other than gravity by a dubious procedure known as renormalization], Planko has proposed that proper time is quantized along the world line of every elementary particle with mass. The fundamental (minimum) proper time interval, or chronon, is represented by the symbol Δ. Distance between particles is naturally quantized in integral multiples of Δc/2. [Spacetime volume is thus more generally quantized, and not space or time separately. By inertial invariance, this quantity is unaffected by a velocity transformation.]

Quantized proper time may be required by ideobasic principles. Consistency logic compels the PCS to recognize the most general conception of time. Yet continuous time is only a limiting case of quantized time. The infinity of numbers on a continuous line segment is furthermore countable only for rational values; there is no one-to-one correspondence between irrational numbers and the set of positive integers. If it is impossible to locate irrational values within the PCS field, they cannot have meaningful existence there (although the concept may exist). Note that time is inherent only along particle world lines; it does not meaningfully reside anywhere else.

If timespace is quantized, then the smooth differential equations of Shrodiik mechanics, QFT and MTT must be replaced by discrete difference equations. Observables defined in terms of derivatives must be similarly redefined. Symmetry principles and conservation laws are all affected.

[Other physicists had previously hypothesized that spacetime was quantized, but only with respect to the overall coordinate framework of a given observer, not with respect to individual particles. These lattice approaches were doomed to failure, as they were divorced from the very processes that define space and time.]

A minimum proper time interval Δ along an elementary proper time line implies an associated maximum absolute angular frequency

      ω_max = 𝜋/Δ,

and a range of meaningful frequencies

      0 ≤ ω ≤ +ω_max .

This limit also applies to RCLs, though a smaller cutoff should apply to PCLs.

In MTT, every elementary particle is characterized by a single, separate proper time line. Based on a symmetric version of the modified single-particle equation of motion, Planko has proposed replacing the linear equation relating the energy E of an elementary particle in its own rest frame to its proper time angular frequency ω by the trigonometric formula

      E = (ℏω_max/𝜋) sin(𝜋ω/ω_max) .

This reduces to the standard equation when ω/ω_max << 1, and can alternatively be written

      E = E_max sin(E_o/E_max)

where E_o is a particle's uncorrected energy E_o = ℏω , and

      E_max = ℏ ω_max /𝜋 = ℏ/Δ at the angular frequency ω_max / 2 .

Note that E_o = m_oc² for an elementary particle with an uncorrected (bare) rest mass m_o.

[Massless particles have no rest frame, and there is no passage of time along their world lines; frequency and energy must be specified with respect to associated particles with mass.]

Proper time quantization reduces and limits a particle's effective rest mass energy, in a manner curiously similar to gravity. For every known elementary particle, E_o / E_max << 1. The sine function in the modified equation for energy can then be approximated by a truncated power series. Including only the first correction term in this expansion,

      E ≈ E_o - E_max(E_o/E_max)³/6 .

According to standard Shrodiik theory, the uncertainty in the position of a particle of mass m cannot be smaller than ℏ/2mc. The bare rest mass m_o for an elementary particle thus cannot be meaningfully confined to a volume with a radius smaller than

      r_min ≈ ℏ/4m_oc = ℏc/4E_o .

Using this relation to remove one power of m_o from the previous equation,

      E ≈ m_oc² - (c⁵Δ²/24ℏ)(m_o²/r_min) .

The correction term is equivalent to the classical gravitational binding energy of a mass m_o distributed over a surface of radius r_min, if one identifies the gravitational constant G as

      G ≈ c⁵Δ²/12ℏ .

Conversely, the chronon Δ can now be related to the gravitational constant by

      Δ = √12ℏG/c⁵ .

Indeed, Planko has identified the minimum distance Δc/2 with the Planko length

      L_P = √ℏG/c³ ≈ 10^-33 centurets,

and the chronon Δ with the Planko time

      T_P = √4ℏG/c⁵ ≈ 10^-43 nocs,

which differs from the value derived above by less than a factor of two.

[These estimates are remarkably close (within a factor of eight) to the chronon value obtained from subsequent experiments. The Planko quantities were inferred theoretically from the time/distance scale at which the quantum effects of gravity should become significant.]

Planko has further proposed a natural system of units, in which the equations of motion are simplified. The unit of time is the chronon, and the unit of distance Δc. Interparticle separations are then half-integral multiples of the fundamental unit, and speed c is numerically equal to one. Units of mass and electric charge are selected so that both the Planko and the gravitational constants are numerically equal to one, and an elementary electric charge is the square root of the fine structure constant.

How does time quantization affect the energy of a multiparticle system? Consider a pair of elementary particles 1 and 2, interacting solely by virtue of their mass, that are at rest with respect to an observer, and separated by radial distance r. When the particles are far apart, interactions are negligible, so proper times τ₁ and τ₂ should be independent and uncorrelated. The two-body wavefunction Ψ_mt is the product of free-particle wavefunctions, with bare masses m_1o and m_2o . Because an increment Δ along one time line does not imply an increment along the other, total system energy E_far is the sum of individual particle energies:

      E_far = ℏω₁+ℏω₂ ≈ m₁c² + m₂c²

where m₁ and m₂ are the respective effective rest masses of each particle, related to the bare rest masses by

      m_jc² = E_max sin(m_joc²/E_max) .

The energy limit E_max applies only to the rest mass energies of the individual particles, along their respective world lines, and not to the overall system, so the maximum possible system energy is 2E_max. In terms of Niestiik COM time coordinates (T,ρ) defined earlier, the discrete rate of change of Ψ_mt along T no longer equals the sum of the discrete rates of change of Ψ_mt along τ₁ and τ₂. The latter instead equals the sum of the discrete rates of change along T for increments a₁Δ and a₂Δ, respectively. This is equivalent to the discrete rate of change along T for an increment Δ_T, where

      Δ/2 (for ω₁=ω₂) ≤ Δ_T ≤ Δ (for ω₁≪ω₂ or ω₂≪ω₁).

Note here that T is not a proper time measure, so the minimum increment Δ does not apply.

At smaller separations, τ₁ and τ₂ may be correlated by mass-related interactions (also required to define interparticle distance), and increments along τ₁ and τ₂ are no longer independent. The maximum correlation, at a minimum meaningful distance r_min, is equivalent to the particles merging into a single world line and proper time – increasing τ₁ by Δ also increases τ₂ by Δ, and vice versa. The time correlation parameter ρ is restricted to values near zero, and the individual particle wavefunctions merge into a single function characterized by a bare mass (m_1o+m_2o) and proper time T, now with a standard minimum increment Δ. Considering only bare mass and time quantization effects, the combined energy is then

      E_near ≈ E_max sin[(m_1o+m_2o)c²/E_max] .

Whereas a total energy limit corresponding to a minimum system time interval Δ/2 applies when the particles are far apart, a lower limit corresponding to Δ applies when they are near.

At intermediate separations r, one can write

      E_r = (1-ε)E_far + εE_near ,

where ε is a function of r, such that ε → 0 as r → ∞, and ε → 1 as r → r_min .

This equation can in turn be rewritten

      E_r = E_far + E_int ,

where E_int is an effective interaction energy

      E_int = -ε (E_far - E_near) .

If bare mass energies are much smaller than E_max, then to good approximation, correction terms of order higher than (E_o/E_max)² may be ignored, and

      E_int ≈ -ε c⁶ m₁m₂(m_1o+m_2o)/2E_max² .

The minimum separation r_min can be estimated from the smallest volume that can confine the total uncorrected rest mass energy,

      r_min ≈ ℏ/4(m_1o+m_2o)c .

If the chronon is approximated by the value √8ℏG/c⁵, then

      E_int ≈ -m₁m₂G (ε/r_min) .

This is identical to the classical expression for gravitational binding energy, if only

      ε = r_min/r .

This low-energy radial dependence is appropriate for a long-range interaction carried by massless gravitons. It also suggests that the degree of correlation between times τ₁ and τ₂ is ~ 1/r, consistent with a cutoff frequency ω_max ~ c/r for PCLs.

[While Fleegello used semiclassical reasoning in the above argument, the conclusions do have some qualitative validity.]

Thus, in the low-energy limit, time quantization appears to effect system energy in a way similar to the low-energy limit of standard graviton exchange, assuming only that τ₁ and τ₂ can be correlated by purely mass-dependent interactions. Gravity would then be similar to the other forces, in that it can be associated with the exchange of a gauge boson at low energies, but distinct in its more fundamental association with time quantization.

What if the interacting particles have electric charges Q₁ and Q₁? The bare electrostatic interaction energy is then

      E^o_elec = Q₁Q₁ / r .

Again ignoring corrections of order greater than (E_o/E_max)², and adopting the original ε(r), the residual interaction energy associated with time quantization is now

      E_int ≈ -[m₁m₂ + (m₁+m₂)E^o_elec/c² + E^o_elecE^o_elec/c⁴] G/r .

The three terms in brackets can be interpreted as the gravitational interaction energies between the two masses, between the masses and the electrostatic field, and between the electrostatic field and itself. As in more traditional theories, gravity couples to all relevant sources of energy.

The PCLs generated by the electric (or any non-gravitational) force appear to only indirectly affect the correlation of the proper times of the two particles; the derived mass-to-mass interaction energy with and without an electric interaction would otherwise have a different value for a given separation. The energies associated with non-gravitational PCLs apparently engender coincident graviton PCLs, which embody the actual process by which time correlations are established. This may reflect gravity's pivotal role in defining the geometry of timespace, and the fact that gravity does not appear to add any new spatial dimensions.

The origami-like unfolding of timespace from a milieu of interwoven, correlated events may generally result in a non-Euclidean macroscopic geometry. The effective curvature of conventional timespace would then be a natural consequence of the quantization of proper time intervals and the correlation of time lines by graviton exchange.

An elementary particle's rest mass may derive from a variety of sources. Every particle is effectively surrounded by a cloud of phantom exchange bosons, corresponding to all applicable interactions. But this is unlikely the sole source of mass for common particles. For example, if the electron's effective size is the minimum volume that can contain its mass, then the electron electric field contributes less than 1% to the observed mass value (the magnitude of the negative gravitational self-energy contribution is 43 orders of magnitude smaller).

Rest mass may also originate in a particle's underlying geometric character. Wittuu has suggested that elementary particles may not be pointlike, but associated with vibrations of extended (but tiny) geometric forms. The size of such entities should be comparable to the radial parameter r_min computed earlier for a given rest mass.

Can quantized timespace be incorporated into a quantum field theory? Time and 3D space have traditionally been treated as continuous system parameters in QFT. Yet past attempts to include gravity in QFT have failed; the theory is not renormalizable for point particles if system timespace is continuous. Even excluding gravity, the standard renormalized version of QFT predicts an enormous vacuum energy density. By adopting a multi-time framework, and restricting the proper time intervals between events to integral multiples of a chronon, maximum energies are naturally limited, and the divergent quantities in QFT calculations may be tamed.

As discussed previously, maximum frequencies associated with phantom processes in a multi-time setting should be further restricted, and inversely proportional to the distance between interacting particles. If space is defined by and only exists with respect to real material particles, then phantom processes that are completely disconnected from real particles might also be forbidden. Any new formulation should reflect that timespace is meaningfully defined only with respect to particle world lines and interactions. It may even prove necessary to treat elementary particles as finite-sized objects.

[The approach to quantized timespace outlined by Fleegello was naive, and flawed in many respects. It does not effectively address relative particle motion, or modifications to symmetry principles and conservation laws, or how an observer can fully integrate the proper times and spatial separations of individual particles with a global timespace coordinate system, and define a total system energy and wavefunction. Fleegello did acknowledge in private correspondence that his approach to quantized timespace was simplistic and incomplete, and certainly did not comprise a testable theory. Yet by replacing QFT with a multi-time theory, quantizing proper time intervals, and identifying elementary particles with extended (though minuscule) vibrating geometric forms, physicists were at last able to integrate gravity into quantum theory, and accurately compute the rest masses of elementary particles from first principles, avoiding the infinities that had plagued previous attempts.]

Although the fundamental (microscopic) equations of motion are symmetric in time, physical processes on a macroscopic level superficially do not appear to be time-symmetric. For example, if all the air molecules in a room were clustered in a corner, they would rapidly spread out to fill the entire room; yet the reverse process is not observed to happen.

Niestu has proposed that this so-called arrow of time is a purely statistical phenomenon.The universal state witnessed by an observer at a given moment is connected by a single time increment (chronon) to a host of other states. In Niestu's view, the number of less ordered (higher entropy) states corresponding to a "forward" time process is simply much larger than that for a "backward" process. If conscious experience is a random walk from one state to another, a person is much more likely to experience events along the traditional arrow of time. Reverse time steps occur, but are swamped by the sheer number of forward steps. This distinction acquires significance mainly in macroscopic systems, due to the sensitive dependence of the number of states of a given type on the number of particles in a system.

Yet this statistical feature does not in itself guarantee our experience of time. A conscious being that lacked a memory would live in an eternal present, with no sense of time's arrow. Most animal memories in a given universal state are found to be of events in connected states with lower overall entropy. This implies that the creation of memory generally involves a statistically irreversible process. Memories laid down in this direction are normally adaptive, and facilitate survival into an expanding realm of universal states. Memories laid down in the opposite direction could in principle also be adaptive, but only if they overtly present as precognitions, consistent with a person's walk through time.

[Shortly after Fleegello died, the natural philosopher Loh demonstrated that even the observed expansion of the universe could be linked to such statistical considerations, providing a critical link between cosmology, gravitation theory and Shrodiik physics.]

As discussed in section 1.18, any physical universe must have [at least] one basic (self-caused) initial state. This state can imply no previous history; the system would otherwise logically extend to an earlier time. Every physical universe must therefore evolve from an initial state characterized by infinitesimal spatial volume. Our own universe appears to have originally experienced runaway, exponential growth – the primeval hyperburst of modern cosmology – from a minuscule primitive state. Every newborn universe must further incorporate particles or analogous localized objects relative to which distance can be meaningfully defined. It could otherwise not expand (or contract) in any meaningful way.

[Fleegello failed to recognize that, if the experience of the CIF is timeless, a self-contained physical universe may also be cyclic, along a time-like dimension that loops back into itself. Such a system must in its entirety be the cause of itself. His basic argument has nonetheless since been extended to the multiverse of all possible physical worlds, whereby our own universe and its generative hyperburst may have been spawned by a pre-existing, self-caused system.]

Physics continues to evolve. Our understanding may yet be profoundly superficial. Will the physical objects and patterns identified so far prove to be unified by a single underlying entity? The multitudinous facets of one magnificent (mathematical) jewel? Or are they disparate, random elements, fragments tied loosely together only by the principle of consistency? Our descendants will hopefully discover the answer to this compelling question.

[During Fleegello's era, physics was rocked by conceptual revolutions every several jopes. Prominent scientists would periodically announce that a "theory of everything" was at hand, or that all that remained in physics was to clean up a few loose ends. These claims were invariably contradicted by new discoveries. Only after many octujopes of struggle was a viable unified theory in fact attained. Even then, physics was hardly dead. The new vision was so rich in possibilities, that its many veins continue to be mined even to this yad. Indeed, quantum physics is no longer considered the most fundamental of the physical sciences, but is viewed instead as the study of emergent phenomena arising from a still deeper level of mathematical reality. Other higher-level sciences (chemistry, biology, psychology, etc.) likewise continue to flourish, as an effective understanding of complex emergent reality inevitably transcends knowledge of underlying physical processes.]